Databases

Contents

• Overview
• Simple Records
• Trees
• Collections and Comprehensions
• Transforming Comprehensions
  

Overview

Simple Records

This section provides an introduction to the definition of language construct. All aspects of a new construct are covered, but the construct is rather simple since it supports data records consisting of fields with names and values. The record construct is an example of an integrated language construct since the field values can be any language construct supported by XOCL. Since XOCL is itself open-ended, this allows record field values to be expressed as any language construct including records and those constructs we have not even thought of yet!

Our requirement is for a database containing records. Each record has a collection of fields with a name and a value. A database may be filtered by supplying it with a predicate that expects a record. The result is a new database containing all those fields that satisfied the predicate.



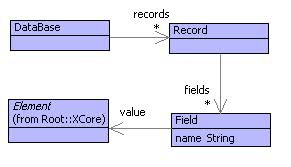
It is usual to start off with a data definition for the elements that are required. Figure  shows the contents of a package called Records. A database consists of a set of records. Each record is a set of fields. Each field has a value that can be of any data type (since Element is the super-class of everything).

The next step is to define a concrete syntax for the Record construct that will synthesize an expresstion whose evaluation produces an instance of the class Record. The complete grammar for Record is defined below, followed by a step-by-step description:

When a syntax construct starts with the token @Record, XMF looks for a grammar associated with the class Record. If it finds one then the grammar should have a rule with the name Record; this rule is the starting point for the parse.

The rule named Record defined above, creates an expression named r that will create a new record when evaluated. The expression r is passed as an argument to the rule named Fields. Once fields has completed its parse, the keyword 'end' is expected. If successful, the value returned by Fields is the result of the parse. So far we have dealt with the following concrete syntax:
The rule Fields deals with the part labelled ??? above. Fields will either recognize nothing (an empty record) or will recognize a sequence of fields separated by commas. If there are fields, the rule uses Field followed by FieldTail, otherwise the rule returns the supplied expression r. Note the repeated use of the variable r in the rule Fields. It is used as a formal argument, a modified variable, an actual argument and in the body of an action.

A field is defined by the rule Field, it is a name n, followed by = followed by an expression e. If successful, it synthesizes an expression that adds a field to the supplied record r. So far, the following can be recognized:
FieldTail is used to allow more than one field to be recognized. A FieldTail is either a comma followed by some fields (notice how the record expression is threaded through so that it is continually built up), or is nothing.

The grammar is complete and the following records can be recognized and the appropriate expressions synthesized:
which synthesizes the following expression:

Trees

Information often naturally forms a tree structure where each component of information is related to several children. Think of company structures: responsibilities from CEO downwards or groupings from the board down. Trees are often used to model physical entities such as cars where a car consists of a body, an engine, electrical system, interior etc. and where a body consists of doors, a windscreen etc.

Trees are useful when we want to organise a model in terms of parent-child relationships which may be physical containment or may be logical groupings (think of nested sets). This section gives an example of a language for expressing trees for classification.

Consider a collection of bank records that are to be classified with respect to awarding a loan. The first step to awarding the loan is to determine an income threshold. If the applicant does not have an annual salary of four times the loan amount then the loan is denied.

The next step is to consider the current debt position of the applicant. If the applicant has debts of more than £10K then the loan is denied. If they have debts of £5 - £10K then the loan application is referred otherwise the application might be awarded.

Finally, if the applicant has an account with the bank, then the loan is awarded otherwise it is referred.



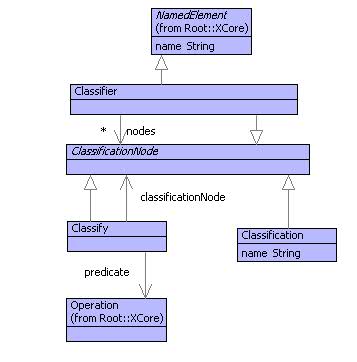
Figure  shows a simple model of a classification tree. A classifier is a named element (so that it can be put in name spaces and then referred to from elsewhere). A classification is a property of some data (for example Award the loan, Deny the loan or Refer the loan). Finally, a classify, is something that applies a predicate to some data to determine whether the classification given by the classificationNode applies.

To construct a classification tree, proceed as follows. Start with a classifier node. Its child nodes, will be classify nodes with disjoint predicates. The child node of a classifier node will be either a classification or another classifier. Proceed with the tree until all categories are classified.

The following example shows a classifier for a loan:
The operation loan accepts a bank and a loan amount. It returns a classifier for the amount. The classifier first checks that the applicant has an adequate annual salary for the required loan. If this condition is not met then the application is denied. Otherwise, the amount of debt is analysed. There are three outcomes: the first denies the application; the second refers the application and the third analyses the bank of the applicant. If the bank of the applicant is the same as that receiving the application then the load is awarded otherwise the application is referred.

The operation loan may be applied to any number of banks and loan amounts. In each case it returns a different classifier.

The classification language is defined by adding a grammar to each of the appropriate classes in the classification model. Each class gets its own grammar so that the classification language is not fixed. The classification language is integrated into XOCL and the components of the language are extensible (new types of classifier node can be defined later and they can be integrated with no changes to the existing components).

Classification is the simplest grammar:
since it recognizes a name and synthesizes an instance of the appropriate class. Classify, involves capturing XOCL expressions and is defined as follows:
Notice that Classify synthesizes an operation definition whose argument name is supplied in tthe classify definition. This is a standard way of capturing executable code (in this case e) within synthesized elements. The body of the operation, e, may refer to any variables that are in scope. The argument n is deliberately placed in scope and allows the body to refer to data that will be supplied by the instance of Classify.

Classification involves sequences of XOCL expressions (an arbitrary number of child classification nodes); it is defined as follows:
The key aspect of the definition above is how the set of child classification nodes is constructed using the Classifications rule. This recognizes nothing, in which case it synthsizes an expression that creates the empty set; or, it recognizes an expression e (a child node definition) followed by more classifications cs and then synthesizes an expression that adds e to cs. This is an example of a recursive rule (The rule is right recursive because the recursive use of Classifications occurs after some input must be consumed. XMF does not support left recursion where Classifications could occur on the left since this would lead to Classifications calling itself without consuming any input) with a base case that creates an empty set.

Collections and Comprehensions

It is usual for data to form collections: employees; customer transactions; connected clients. When modelling collections of data it is very convenient to have language structures that make it easy to create, transform and filter the collections. This section describes how such a language construct can be defined.

A typical example of data collections occurs in a relational database. Figure  shows a portion of a MS Access database containing three tables relating to a pain manufacuring company. The Customers table shows all the customers who have bought paint from the company; each customer has a unique id, a name, an address and a running tally of the number of orders that have ben placed.

The Products table shows all the types of paint that the company sells along with the current price per unit. Finally, the Orders table shows the orders that have been placed, linking customers, products and amount.

Database tables contain records expressed as rows. Each table is modelled as a class and the records modelled as instances of the class grouped together as a set. The diagam in figure  shows three classes corresponding to the three database tables above.



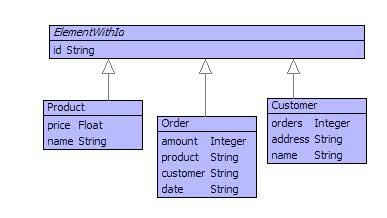
The model above has chosen to represent the database tables directly: each table uses the id field as a primary key and each class has modelled this directly. Unlike database records, objects have a unique identity, so this is not strictly necessary. It is useful to retain the id field to show how database style queries and operations are supported by the collection language construct below.

The database records are modelled as instances of the classes as shown below:
Each table is modelled as a global variable whose value is a set of objects. New records can be added by updating the variable:
The operation newId is defined to automatically calculate a new identifier for a collection of elements. The addCustomer operation modifies the collection of customers by adding a newly constucted customer. Removing customers can be achieved by a similar update to the global variable.

A query on one or more database tables involves performing a test on each of the records in the table and producing a new table as a result. In the model, a table is represented as a collection of elements. The new language construct Cmp (short for comprehension) allows us to do a query as follows:
The operation ordersGreaterThan (1) takes an integer x and returns a collection of customers. Line (2) introduces the query as a Cmp expression that returns all those customers (2) where each customer is an element of the Customers table (3) and for which the orders of each customer are grater than x (4).

A Cmp expression has the following general form:
A clause is either a binding (name <- collection) or a filter (? test). The Cmp expression performs each clause in turn. A binding selects each element from the collection in turn and, for each selection, evaluates the rest ot the Cmp expression. A filter evaluates the test (referencing any names bound tfrom its left); if the test succeeds then evluation proceeds, otherwise evaluation retuns to the last selction and tried with another element.

Consider the definition of ordersGreaterThan again. Line (3) causes each sucessive customer to be selected from the Customers table. Line 4 allows only those customers to proceed whose orders value passes the test. Finally, a sequence is returned containing all those customers (2) that get through the test.

The following is an example of a query that involves multiple binding and filters:
The operation customersWhoBuy is supplied with the name of a product and returns a sequence of customer names for those customers who have bought the supplied product.

A typical operation that occurs in a database is a join where two different tables are joined on two fields with the same value. The records that have been defined so far have ben instances of specific classes. A join does not necessary produce a record with a meaningful type (although it might); section  defines a language construct for representing arbitrary records. The following expression performs a join on the three tables producing a new table of records showing the amount of each product for each customer:


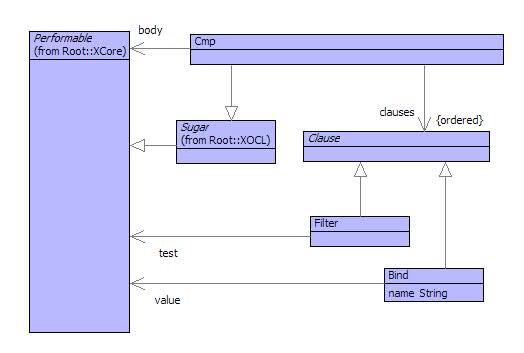
A Cmp expression is defined in terms of a package of syntax classes shown in figure . The class Cmp is defined as sugar which means that it must define an operation called desugar that turns an instance of Cmp into a Performable thing (usually an instance of OCL classes).

A Cmp has a performable body and a sequence of clauses. Each clause is either a binding or a filer. A Cmp is desugared as follows:
The translation of a Cmp expression into basic XOCL is defined by case analysis. Case (1) occurs when there are no clauses. In this case the body is transformed into a single element sequence. Case (2) occurs when there is a single binding. In this case the value of the binding produces a collection and the body is performed for each element of the collection producing a sequence.

Case (3) occurs when there is a binding and some clauses. In this case the following equivalence is used:
Case (4) tests the expression e. If the result is true then the Cmp expression proceeds otherwise it produces no elements. This has the effect of filtering out the current variables that have been bound so far.

Finally, the Cmp expression has a grammar that synthesizes an instance of Cmp that, since it is an instance of Sugar, calls desugar automatically:

Transforming Comprehensions

The previous section has shown how a comprehension expression can be transformed into an XOCL expression, thereby enriching XOCL with a new language construct. Comprehensions have often been proposed as a construct suitable for performing database queries since they abstract away from the details of how the queries are performed and how the result sets are built up.

A comprehension can be viewed as a query over a database if the tables are viewed as sets of records. In this way the queries are performed by selecting records, filtering them with predicates and joining them back together. However, whilst this is an attractive way to construct database queries, it does not solve the problems of how the queries are performed and how the comprehensions can be embedded into a standard programming language.

This section sketches out how comprehensions can be viewed as database queries by showing how to desugar a comprehension into a standard imperative language that provides a database interface. The translation is deliberately simple; once it has been described the conclusion outlines how the translation can be made more realistic.

Instead of the Cmp::desugar operation defined in the previous section, a new operation is defined. The operation is called toSQL and takes two arguments: the an expression to be transformed into an imperative program and a variable. At run-time, the variable will be bound to a set of values; after performing the comprehension program, the set will contain the result.

The toSQL operation proceeds by case analysis on the expression, each case is addressed in turn. The first case deals with the aituation where there are no qualifiers:
The resulting program code creates a new set S and then uses this as the container for the body of the comprehension. The resulting set S is added to the supplied set (value of var). The next case deals with a single filter:
If the predicate expression p is true then the body of the comprehension is performed with the supplied var as the target set. Otherwise the empty set is added to the target var. The next case deals with the situation where there are multiple qualifiers:
The same transformation as before is applied to the comprehension whereby the multiple qualifiers are reduces by nesting the comprehension. In this case the transformation on the nested comprehension will produce an impreative program that updates the supplied set. Therefore, after the supplied set is updated it is flattened before returning it. Finally, the case where variables are bound is dealt with as follows:
Here it is assumed that all bindings select their elements from named database tables. In this case the result set S is constructed by calling a builtin procedure DB.SQL that takes an SQL query as a string. A for-loop is used to iterate through the result set and the body of the loop is generated by translating the body of the comprehension. Notice that the set supplied to the body translation is P - the new set created as part of the binding. The final action is to add the set P to the supplied set var.